ピタゴラスが発見した「音楽」と「数字」の意外な関係
2018年06月05日 公開 2024年12月16日 更新
調和する音には数学的な規則性があった
彼らはまずモノコードと呼ばれる楽器を発明しました。
モノコードというのは共鳴箱の上に弦を一本張って、琴柱(ことじ)を移動させることによって、振動する弦の長さを変えられる図のような装置のことです。
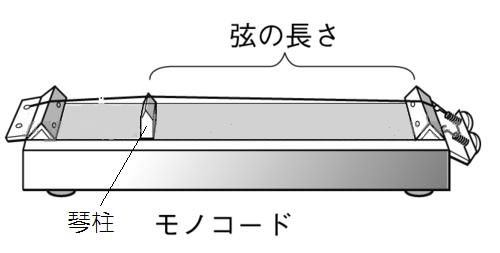
ピタゴラスたちは、このようなモノコードを2つ用意しました。
実験の方法はこうです。
片方のモノコードの弦の長さは固定しておきこれを基準にします。もう一方のモノコードは琴柱を動かすことで弦の長さを短くしていきます。そうして2つの弦を同時に弾き、綺麗に響き合う位置を探します。すぐに、片方の弦の長さが半分になったとき、すなわち弦の長さが2:1になったときに2つの音が完全に溶け合うことがわかりました。
ピタゴラスたちはその後、他にも2つの音が調和する場所がないかを探しました。すると、2つの弦の長さの比が3:2や4:3のときにもそれぞれ2つの音はよく調和することがわかりました。
音程の美しさは「神のイタズラ」?
「ドレミファソラシド」の低いドから高いドまでの音程の幅を1オクターブといいます。1オクターブ離れた2つの音は同時に響くと高さの違う「同じ音」に感じられて、完全に溶け合うことを御存知の方は多いでしょう。
音楽では、音程(2つの音の音の高さの差)を表すときに「度」という接尾辞を使います。ただし「0度」というのはなく、同じ高さの音どうしは「1度」と言います。ドとレのようにとなり合う音は2度、ドとミは3度です。
特に綺麗に響き合う音程には頭に「完全」を付けることになっていて、1オクターブの中に完全音程は、完全4度(ドとファ)、完全5度(ドとソ)、完全8度(1オクターブ)の3つがあります。ピタゴラスたちが発見した3つの「調和する音程」はそれぞれ、次のように3つの完全音程に対応しています。

弦の長さの比が2:1 完全8度(1オクターブ)
弦の長さの比が3:2 完全5度
弦の長さの比が4:3 完全4度
完全8度だけでなく、美しく響きあう音程になるときの2つの弦の長さの比がすべて簡単な整数の比になることに、ピタゴラスたちは感動しました。まるで神様に仕掛けられたイタズラを発見したかのような心持ちになったことでしょう。音程の研究を通して、数字を研究することは神の意思を汲み取ることであり、数字の中にこそ神の言葉があるのだと考えるようになったとしても不思議ではありません。














