電卓に隠された「2220」のミステリー

サイエンスナビゲーターの桜井進氏は、著書『超・超面白くて眠れなくなる数学』にて、身近なところにある“数字”の謎について解き明かす。本記事では、電卓の数の配列による不思議な現象を解決する。

※本稿は、桜井進 著『超・超面白くて眠れなくなる数学』より、内容を一部抜粋・編集したものです。

なぜか答えは　「2220」

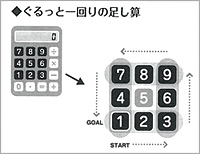
電卓には、いくつもの面白い計算が隠されています。そのうちの１つをご紹介しようと思います。皆さんもお手元に電卓をご用意ください。

電卓の数字キーは「1」から反時計回りに「2、3、6、9、8、7、4」と並んでいます。

この順番通りに並んだ３つの数字を３桁の数として、４つの数をつくっていきましょう。

「1」から始めて「1」に戻る足し算をしてみると、「123＋369＋987＋741」と足していくということです。

そうすると、答えは「2220」になりました。

それでは、次に「2」から始めて「2」に戻る足し算をしてみましょう。「236＋698＋874＋412＝2220」というように、やはり結果は「2220」となります。

同じように、スタートの数字が「3」「6」「9」「8」「7」「4」の場合についても足し算をしてみてください。面白いことに結果はすべて「2220」になるのです。

次は、角の数（1、3、9、7）を、それぞれ３回押した数（３桁ずつ）の足し算をしてみましょう。「111＋333＋999＋777」。やはり結果は「2220」です。

辺の真ん中の数（2、6、8、4）を３桁ずつ足し算してみましょう。「222＋666＋888＋444」。やはり結果は「2220」です。

では、対角線の３つの数字を３桁の数として、４つの数を足し算してみると、どうでしょうか。「159＋357＋951＋753＝2220」。またもや「2220」になりました。

最後に十字の３つの数字を３桁の数として、４つの数を足し算します。「258＋654＋852＋456＝2220」。なんとこれも「2220」です。

読者の皆さんも、電卓を片手に「ぐるっと一回りの足し算」、そして「角」「辺の真ん中」「対角線」「十字」の足し算をしてください。その次に、計算を紙に書いて、足し算を確かめてみてください。

どうしてすべての足し算が「2220」になってしまうのか――。紙に書いた計算をもとに、その謎に迫りましょう。