ビジネス数学教育家が「誰の人生においても数学は必要」と断言する理由

数学をするときの「頭の使い方」は様々な場面で必要となる

数学をするとは、単なる計算問題を暗記した公式に当てはめて機械的に答えを出す行為ではありません。この例で挙げたような「アルバイトの給与」とは何か、といった問題を深く正しく考え、答えを出す行為なのです。

これからの人生であなたが数学の計算問題を解くことは、ほとんどないでしょう。しかし、このような頭の使い方を必要とする場面は多々あるのではないでしょうか。

例えば、ビジネスパーソンなら意思決定を必要とする場面はたくさんあるでしょう。仮にあなたが新卒社員を採用する面接官だとします。採用の可否を判断する、まさに意思決定があなたの仕事です。

おそらくあなたは「いい新卒人材ってどんな人?」という問いを立てるのではないでしょうか。

仮に「コミュニケーション能力が高くて、3年後もその会社で活躍するイメージが具体的にある学生」と定義すると、その条件は「コミュニケーション能力（X）」と「3年後のイメージ（Y）」に分解できます。

さらにこのXとYを比較し、どちらの優先順位が高いかを評価します。

仮にXのほうが優先順位が高いとするなら、結論として「採用する人材の条件はXかつYであり、かつXの素養がより高い人物を優先する」というはっきりした型（モデル）ができます。型ができるからあなたは意思決定ができる。すなわち答えを出せるのです。

いかがでしょう。数学の問題を解くことはなくても、数学をするときの頭の使い方は必要とする。もしあなたがビジネスパーソンなら、数学的に考えない日など1日たりともない──これが私の持論です。

余談ですが、数学を理解できた方がよく「数学と哲学は似ていますね」といった類の言及をされます。もしかしたらあなたも、これまでの人生の中でそんなことを言う人物に出会ったことがあるかもしれません。

念のため説明しますと、哲学とは人生・世界、事物の根源のあり方・原理を、理性によって求めようとする学問のことです。

恋愛とは何か。就職活動とは何か。通勤電車とは何か。アルバイトの給与とは何か。いい人材とは何か。

これだけの「問い」を発していますが、まさに根源のあり方・原理を求めようとするものではないでしょうか。数学と哲学は似ている。その真意はこんなところにあるのです。

ではここまでのおさらいということで、ひとつエクササイズをしてみましょう。

【演習問題】
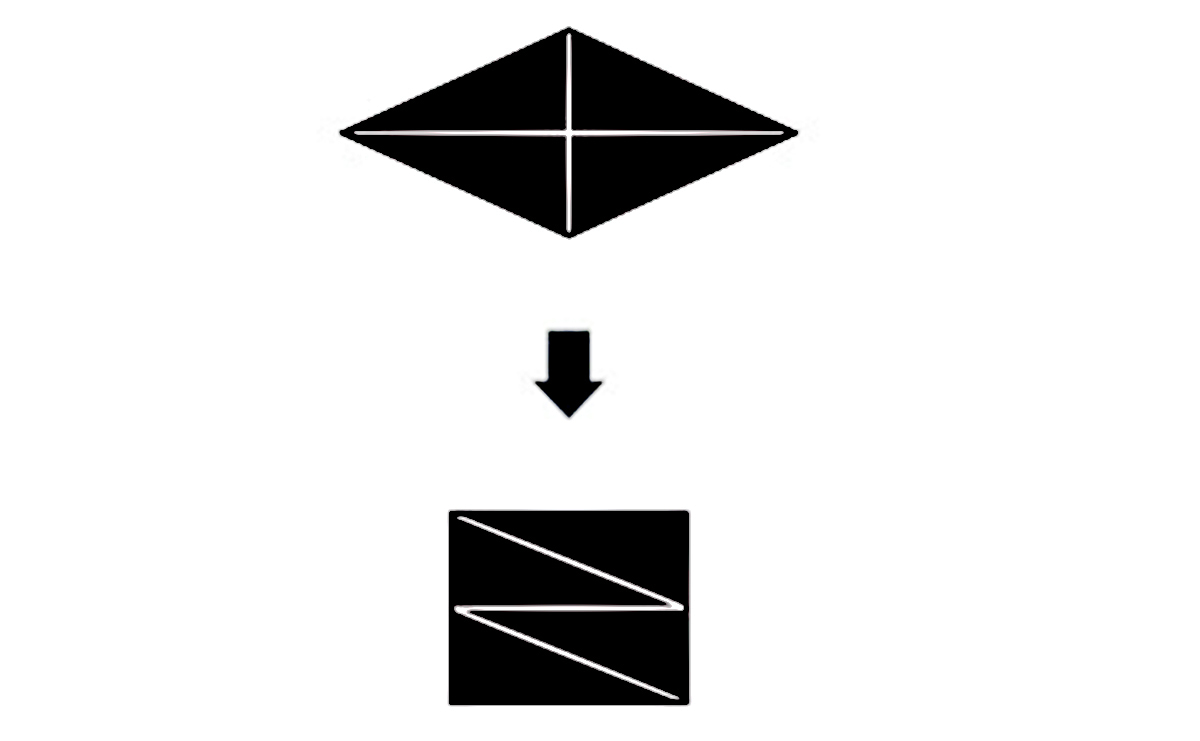
「このひし形の面積の求め方」を小学生に説明してください。

実際に計算する必要はありません。その説明に「定義」「分解」「比較」「構造化」「モデル化」といったものが使われていることが確認できればOKです。ちなみに子供は、「面積ってなぁに?」といった類の質問を平気でしますのでご注意ください（笑）。

【回答例】

・STEP1　まず「面積」を定義する
「面積」とは平面図形の大きさ、広さ、の量のことである（定義）

・STEP2  「与えられた図形」を分析する
4つの直角三角形に分解できる（分解）
その4つは同じ面積である（比較）

・STEP3　構造を把握し、面積を求める
その4つを並べ替えることで、この図形はシンプルな長方形に変換できる。長方形の面積は（縦の長さ）×（横の長さ）であり、図形の面積が求まる